Здравствуйте, уважаемый Григорий!Поскольку вы отвечаете не сразу, я потратил фактически полдня на анализ ваших формул и соответствующих примеров и все выяснил, что исключает дальнейшие мои к вам вопросы.
Григорий писал(а):
Вы всё пытаетесь доказать недоказуемое:
(1) Y = ЗАРПЛАТА + ПРИБЫЛЬ = Const при росте уровня оплаты труда.
Ниже приведено доказательство того, что равенство ЗАРПЛАТА + ПРИБЫЛЬ = Const НЕ ВЫПОЛНЯЕТСЯ при изменении уровня оплаты труда, если при этом объёмы производства и технологии производства фиксированы.
Изменение в уровне оплаты труда приводит всегда к изменению величины Y.
В экономике с простым воспроизводством агрегат Y равен цене выпуска второго подразделения (цене конечного продукта):
(2) Y = p2 * X2
Здесь p2 – цена единицы продукта второго подразделения («жизненных средств»), X2 – выпуск продукции второго подразделения (в натуральном измерении).
Поскольку мы рассматриваем простое воспроизводство, то
(3) X2 = Const
Докажем, что цена p2 не может оставаться постоянной при росте уровня оплаты труда w.
Этим будет также доказано, что произведение Y = p2 * X2 тоже не может быть постоянным при увеличении уровня оплаты труда, так как X2 = Const
Пишем уравнения для цен (из модели, которую я приводил в предыдущих сообщениях).
(4) (a0 * p1 + w * l0 * p2) * (1 + r) = 1 – уравнение для денег
(5) (a1 * p1 + w * l1 * p2) * (1 + r) = p1 – цена «средств производства»
(6) (a2 * p1 + w * l2 * p2) * (1 + r) = p2 – цена «жизненных средств»
Решаем эту систему.
Записываем её в матричном виде:
(7) (1;p1;p2) * A = lambda * (1;p1;p2), где (7.2) lambda = 1 : (1 + r)
Компоненты матрицы А:
А(1;1) = A(1;2) = A(1;3) = 0; A(2;1) = a0; A(2;2) = a1; A(2;3) = a2;
A(3;1) = w * l0; A(3;2) = w * l1; A(3;3) = w * l2
Уравнение (7) – это уравнение на собственные значения матрицы A. Ненулевые решения существуют, если равен нулю определитель матрицы A – lambda * I, где I – единичная матрица.
(8) Det[A – lambda * I] = 0
Уравнение (8) приводится к квадратному уравнению относительно неизвестной lambda:
(9) (-lambda) * [(lambda)^2 - (a1 + w*l2)*lambda + w*(a1*l2-a2*l1)] = 0
Приравнивая нулю множитель в квадратных скобках, находим:
(10) lambda = [a1 + w * l2 + КОРЕНЬ({a1 + w*l2}^2 – 4 * w * (a1 * l2 – a2 * l1))]/2
Учитывая (7.2), находим норму прибыли:
(11) r = 1/lambda – 1
Осталось найти компоненты вектора цен.
Делим уравнение (5) на уравнение (6) и вводим вспомогательную переменную:
(12) t = p2 : p1
Получаем уравнение относительно t:
(13) (a1 + w * l1 * t) : (a2 + w * l2 * t) = 1 : t
Это уравнение сводится к квадратному уравнению:
(14) w*l1*t^2 + (a1 – w*l2)*t - a2 = 0
Отсюда находим t:
(15) t = [w*l2 – a1 + КОРЕНЬ((a1 – w * l2)^2 + 4*w*l1*a2)] : (2 * w * l1)
Учитывая (12), выражаем p2 через р1:
(16) p2 = p1 * t
Осталось найти p1. Для этого используем уравнение (4), которое можно интерпретировать как условие нормировки вектора цен. Вынося в левой части p1 и учитывая (12) получаем:
(17) p1 = lambda : [a0 + w*l0*t]
РЕШЕНИЕ:
(R1) lambda = [a1 + w * l2 + КОРЕНЬ({a1 + w*l2}^2 – 4 * w * (a1 * l2 – a2 * l1))]/2
(R2) t = [w*l2 – a1 + КОРЕНЬ((a1 – w * l2)^2 + 4*w*l1*a2)] : (2 * w * l1)
(R3) p1 = lambda : [a0 + w*l0*t]
(R4) p2 = p1 * t
Цена p2 зависит от параметров {a0;a1;a2;l0;l1;l2;w}. Можно написать явный вид этой зависимости, подставив в формулу (R4) выражения (R1) – (R3) – формула получится очень громоздкой. Удобнее при вычислениях использовать формулы (R1) – (R4).
Сначала по заданным значениям {a0;a1;a2;l0;l1;l2;w} находим lambda и t, согласно формулам (R1)-(R2). Подставив их в (R3), находим p1 и подставив p1 и t в (R4) находим p2.
Поскольку цена p2 зависит от уровня оплаты труда w, то ясно, что, если все другие параметры {a0;a1;a2;l0;l1;l2} фиксированы (а значит технологии производства неизменны), изменение уровня оплаты приводит к изменению цены p2, а значит приводит к изменению агрегата p2 * X2, который равен сумме «зарплата + прибыль».
ВЫВОД: Таким образом, если технологии неизменны и значит параметры {a0;a1;a2;l0;l1;l2} фиксированы, изменение уровня оплаты труда (параметра w) приводит к изменению цены «жизненных средств» р2, а значит к изменению агрегата «зарплата + прибыль».
Доказательство завершено.
Условие p2 = Const определяет некоторую взаимосвязь между параметрами {a0;a1;a2;l0;l1;l2;w}:
(R5) p2(a0;a1;a2;l0;l1;l2;w) = Const
Поэтому, если мы преобразуем один числовой пример в другой так, что выполняется условие постоянства суммы «зарплата + прибыль» (Таблицы Валерия), это возможно лишь, если кроме роста уровня оплаты труда w, одновременно меняется хотя бы ещё один параметр. Лишь в этом случае условие (R5) может быть выполнено. Алгоритм выделения технологических коэффициентов, который был приведён в предыдущих сообщениях, устроен таким образом, что при «преобразованиях Валерия» фиксируются все параметры, кроме параметров w и a0. Именно по этой причине изменение w, дающее прирост зарплаты, всегда сопровождается изменением параметра a0, который описывает технологию производства денег. Можно было бы составить другой алгоритм, в котором мы фиксировали бы параметр a0, - тогда изменение w сопровождалось бы изменением какого-то другого параметра технологии. В любом случае, существование зависимости (R5) означает некую взаимосвязь между параметрами, так что меняя один параметр (w) мы тем самым меняем хотя бы ещё один параметр так, чтобы условие (R5) оставалось бы выполненным.
Рассмотрим, однако, числовой пример. Предположим, что сам господь бог решил распределить 300 единиц конечного продукта между рабочими и капиталистами в пропорции 175 : 125. Затем он, усмотрев некоторую несправедливость, решил добавить рабочим 10%, разумеется, отняв соответствующее количество у капиталистов. В итоге получилось 192,5 : 107,5. При этом сумма слагаемых не меняется
175 + 125 = 300 = 192,5 + 107,5.
Из этой всей божьей благодати запомним, что увеличение дохода рабочих на 10% с экономической точки зрения означает увеличение их доли в конечном продукте с 175/300 = 58,33% до 192,5/300 = 64,17%.
А теперь посмотрим на таблицу, в которой я заново вычислил и разместил параметры «основного преобразования Григория»:
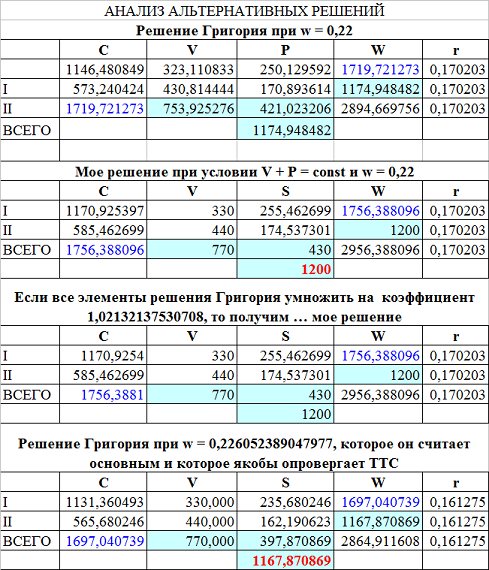
Анализ альтернативных решений сведен в таблицу:
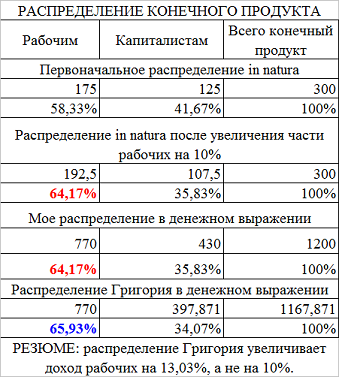
Анализ показывает, что из альтернативных решений основное решение Григория ошибочно и, руководствуясь божьим промыслом, оно должно быть изгнано из храма науки. Ошибка Григория состоит в том, что он увеличил реальную зарплату не на 10, а на 13,03%, у него доля рабочих в конечном продукте составляет 65,93%, а надо, чтобы она составляла 64,17%.
Вторая ошибка Григория заключается в том, что он вдруг начинает в моем решении вычислять параметр а0 и его значение у него получается 0,13944195 вместо 0,14722222.
Хотя я никогда не использовал этот параметр для расчетов (более того, его нельзя менять, так как он исходный), тем не менее, мне приписывается большой грех, заключающийся в изменении технологии производства самих денег!
Григорий, правда, интуитивно чувствует неладное, утверждая:
Цитата:
Можно было бы составить другой алгоритм, в котором мы фиксировали бы параметр a0, - тогда изменение w сопровождалось бы изменением какого-то другого параметра технологии.
Утверждение, однако, мягко говоря, ошибочное. Вернее было бы утверждать об изменении цены производства самих денег.
Воспользуется формулой Григория и подставим в нее численные значения параметров из моего решения (вторая таблица на рисунке):
(20) (a0 * p1 + w * l0 * p2) * (1 + r) = 1
(0,14722222* 2,341850795 + 0,22*0,6*4)*(1+ 0,1702035) = 1,02132137530708.
Как видим, в моем решении цена производства денег увеличена в 1,02132137530708 раза, а технологический коэффициент a0 остается без изменения.
Надеюсь, теперь понятен смысл коэффициента 1,02132137530708, который был ранее представлен на рисунке (третья таблица). С помощью этого коэффициента цена производства конечного продукта увеличена до уровня его стоимости.
Здесь я сделаю паузу, в надежде услышать возражения Григория.
С уважением,
В.К.



